Hello World
hello world
hello world
We developed an cross-platform, integrated, and graphical Java app based on JavaFX for BNDSer to practice AP CSA FRQs.
You can download the release at https://github.com/Link-BNDS/CSA_Practice_APP/releases/tag/AP . You can also find the src at repo https://github.com/Link-BNDS/CSA_Practice_APP.
The description can also be found at that repo.
Thanks for your support.
在Coursera上吴恩达的Machine Learning中,Logistic Regression作为初学者们接触到的第二个模型,其本身是非常重要的。但是在课程当中其损失函数的梯度公式则被一笔带过。而很多人都对其为什么与线性回归的损失函数梯度是一样的表示好奇,因此,我特地从头推导了这一式子。
The "Machine Learning" course on Coursera is a one of the most popular course over all of MOOC. This course is famous for its simplified teaching step and other bright spots. Logistics regression, as the most important model for beginner, lacks appropriate detailed derivation of formula. In this blog, I am going to expound this section step by step.
I think most of you have already got familiar with logistic regression.
As we all know, the cost function of the logistic regression is modified from the one from linear regression model. \[ Cost\left( h_{\theta}\left( x \right) ,y \right) =\left\{ \begin{aligned} -\log \left( h_{\theta}\left( x \right) \right) \,\, if\,\,y&=1\\ -\log \left( 1-h_{\theta}\left( x \right) \right) \,\, if\,\,y&=0\\ \end{aligned} \right. \]
To simplify this function, we can write it as
\[ J\left( \theta \right) =\frac{1}{2m}\sum_{i=1}^m{Cost\left( h_{\theta}\left( x^{\left( i \right)} \right) ,y^{\left( i \right)} \right)} \]
which
\[ Cost\left( h_{\theta}\left( x^{\left( i \right)} \right) ,y^{\left( i \right)} \right) =-y^{\left( i \right)}\log \left( h_{\theta}\left( x \right) \right) -\left( 1-y^{\left( i \right)} \right) \log \left( 1-h_{\theta}\left( x^{\left( i \right)} \right) \right) \]
And next, is the part I want to expound. Andrew, in this MOOC, just briefly introduce that the gradient of the new cost function is the same as the one for linear regression. There is no explicit derivation here.
For cost function \(J\), we can write it as
\[\begin{equation} \begin{aligned} J\left( \theta \right) &=-\frac{1}{m}\left[ \sum_{i=1}^m{-y^{\left( i \right)}\log \left( h_{\theta}\left( x \right) \right) -\left( 1-y^{\left( i \right)} \right) \log \left( 1-h_{\theta}\left( x^{\left( i \right)} \right) \right)} \right] \\ \frac{\partial}{\partial \theta _j}J\left( \theta \right) &=\frac{\partial}{\partial \theta _j}\left[ -\frac{1}{m}\left[ \sum_{i=1}^m{-y^{\left( i \right)}\log \left( h_{\theta}\left( x \right) \right) -\left( 1-y^{\left( i \right)} \right) \log \left( 1-h_{\theta}\left( x^{\left( i \right)} \right) \right)} \right] \right] \\ &=-\frac{1}{m}\left[ \sum_{i=1}^m{\left( y^{\left( i \right)}\frac{1}{h_{\theta}\left( x^{\left( i \right)} \right)}\cdot \frac{\partial}{\partial \theta _j}h_{\theta}\left( x^{\left( i \right)} \right) +\left( 1-y^{\left( i \right)} \right) \cdot \frac{1}{1-h_{\theta}\left( x^{\left( i \right)} \right)}\cdot \frac{\partial}{\partial \theta _j}\left( -h_{\theta}\left( x^{\left( i \right)} \right) \right) \right)} \right] \\ &=-\frac{1}{m}\left[ \sum_{i=1}^m{\left( y^{\left( i \right)}\frac{1}{h_{\theta}\left( x^{\left( i \right)} \right)}-\left( 1-y^{\left( i \right)} \right) \cdot \frac{1}{1-h_{\theta}\left( x^{\left( i \right)} \right)} \right) \cdot \frac{\partial}{\partial \theta _j}\left( h_{\theta}\left( x^{\left( i \right)} \right) \right)} \right] \\ &=-\frac{1}{m}\left[ \sum_{i=1}^m{\left( y^{\left( i \right)}\frac{1}{g\left( \theta ^Tx \right)}-\left( 1-y^{\left( i \right)} \right) \cdot \frac{1}{1-g\left( \theta ^Tx \right)} \right) \cdot \frac{\partial}{\partial \theta _j}\left( g\left( \theta ^Tx \right) \right)} \right] \end{aligned} \end{equation}\]
In logistic regression, we use the logistic function as our decision function. Therefore, (Mentioned: \(T\) refers to transpose)
\[\begin{equation} \begin{aligned} \frac{\partial}{\partial \theta _j}g\left( \theta ^Tx \right) &=\frac{\partial}{\partial \theta _j}\cdot \frac{1}{1+e^{-\theta ^Tx}} \\ &=\frac{\partial}{\partial \theta _j}\left( 1+e^{-\theta ^Tx} \right) ^{-1} \\ &=-\left( 1+e^{-\theta ^Tx} \right) ^{-2}\cdot e^{e^{-\theta ^Tx}}\cdot x \\ &=-\frac{e^{e^{-\theta ^Tx}}\cdot -x}{\left( 1+e^{e^{-\theta ^Tx}} \right) ^2} \end{aligned} \end{equation}\]
We set \(k=e^{-\theta ^Tx}\), plug it in,
\[\begin{equation} \begin{aligned} &=\frac{k}{\left( 1+k \right) ^2}\cdot x \\ &=\left( \frac{1}{1+k}\cdot \frac{1+k-1}{1+k} \right) \cdot x \\ &=\left[ \frac{1}{1+k}\cdot \left( 1-\frac{1}{1+k} \right) \right] \cdot x \end{aligned} \end{equation}\]
Bring it back, we can see we construct the logistic function itself,
\[\begin{equation} \begin{aligned} &=\left[ \frac{1}{1+e^{-\theta ^Tx}}\cdot \left( 1-\frac{1}{1+e^{-\theta ^Tx}} \right) \right] \cdot x \end{aligned} \end{equation}\]
Thus, we can use the logistic function to simplify the eqution,
\[\begin{equation} \begin{aligned} &=\left[ \frac{1}{1+e^{-\theta ^Tx}}\cdot \left( 1-\frac{1}{1+e^{-\theta ^Tx}} \right) \right] \cdot x \\ &=g\left( \theta ^Tx \right) \cdot \left( 1-g\left( \theta ^Tx \right) \right) \cdot x \end{aligned} \end{equation}\]
We plug back this portion to the gradient of cost function (1),
\[\begin{equation} \begin{aligned} \frac{\partial}{\partial \theta _j}J\left( \theta \right) &=-\frac{1}{m}\left[ \sum_{i=1}^m{\left( y^{\left( i \right)}\cdot \frac{1}{g\left( \theta ^Tx \right)}-\left( 1-y^{\left( i \right)} \right) \cdot \frac{1}{1-g\left( \theta ^Tx \right)} \right)}\cdot g\left( \theta ^Tx \right) \cdot \left( 1-g\left( \theta ^Tx \right) \right) \cdot x^{\left( i \right)} \right] \\ &=-\frac{1}{m}\left[ \sum_{i=1}^m{\left[ y^{\left( i \right)}\cdot \left( 1-g\left( \theta ^Tx \right) \right) \cdot x^{\left( i \right)}-\left( 1-y^{\left( i \right)} \right) \cdot g\left( \theta ^Tx \right) \cdot x^{\left( i \right)} \right]} \right] \\ &=-\frac{1}{m}\sum_{i=1}^m{\left[ y^{\left( i \right)}\cdot x^{\left( i \right)}-y^{\left( i \right)}\cdot g\left( \theta ^Tx \right) \cdot x^{\left( i \right)}-g\left( \theta ^Tx \right) \cdot x^{\left( i \right)}+y^{\left( i \right)}\cdot g\left( \theta ^Tx \right) \cdot x^{\left( i \right)} \right]} \\ &\mathrm{because}-y^{\left( i \right)}\cdot g\left( \theta ^Tx \right) \cdot x^{\left( i \right)}\,\,\mathrm{offsets} +y^{\left( i \right)}\cdot g\left( \theta ^Tx \right) \cdot x^{\left( i \right)} \\ &=-\frac{1}{m}\sum_{i=1}^m{\left[ y^{\left( i \right)}\cdot x^{\left( i \right)}-g\left( \theta ^Tx \right) \cdot x^{\left( i \right)} \right]} \\ &=-\frac{1}{m}\sum_{i=1}^m{\left[ \left[ y^{\left( i \right)}-g\left( \theta ^Tx \right) \right] \cdot x^{\left( i \right)} \right]} \\ &=\frac{1}{m}\sum_{i=1}^m{\left[ \left[ h_{\theta}\left( x^{\left( i \right)} \right) -y^{\left( i \right)} \right] \cdot x^{\left( i \right)} \right]} \end{aligned} \end{equation}\]
which is the same as linear regression's
Q.E.D.
In my second semester of High School Junior year, when we were studying vector calculus @Calculus 3, our teacher gave us an assignment: proof of Stokes formula. CALCULUS EARLY TRANSCENDENTALS EIGHTH EDITION JAMES STEWART (our Calculus3 textbook) only has a special form of stokes' theorem proof. Thus, I looked up the prood at old Chinese Text Book. It is a pity that our high school calculus education with American calculus education are quite different compared to Chinese's. I searched on zhihu, Bilibili and other public platforms, but failed to find any suitable results. Luckily, I finally figure it out when I went back home during the epidemic.
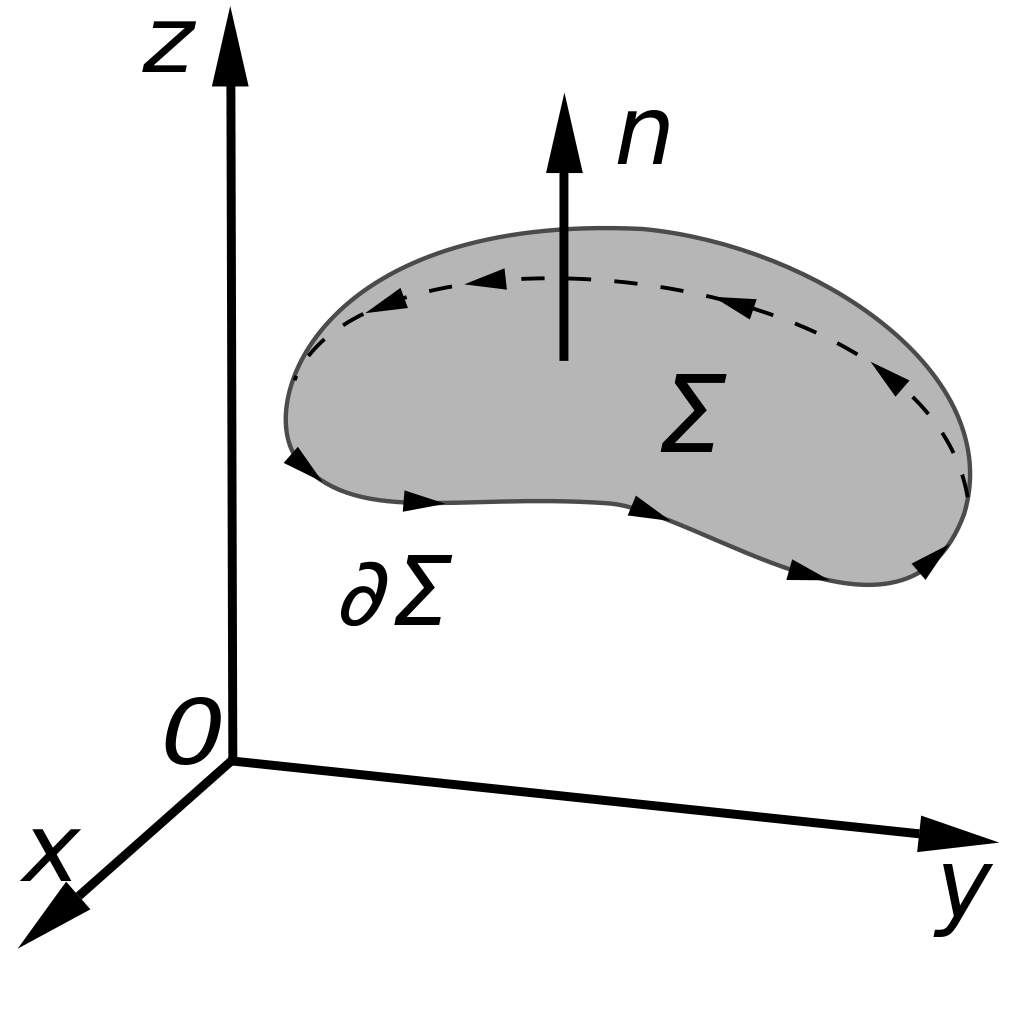
For surface S in \(R^3\) space is an oriented surface in \(x,y,z\) coordinate with boundary \(\partial S\). Let \(R\) be abounded, open region in \(s, t\) plane with smooth boundary \(\partial R\) . Suppose that \(F\) is a continuously differentiable vector field. \(\vec{r}\) is a smooth parametrization that maps \(R\) to \(S\), and \(\partial R\) to \(\partial S\). Then
\[ \iint_S{curl\,\,\vec{F}\,\,·\,\,d\vec{S}}=\iint_S{\left( \nabla \times \vec{F} \right) \,\,·\,\,\vec{n}\,\,dS}=\int_{\partial S}{\vec{F}\,\,·\,\,\vec{T}\,\,ds}=\,\,\int_{\partial S}{\vec{F}\,\,·\,\,d\vec{r}} \]
Let
\[ \vec{r}\left( s,t \right) =\left[ \begin{array}{c} x\left( s,t \right)\\ y\left( s,t \right)\\ z\left( s,t \right)\\ \end{array} \right] \,\,: R\rightarrow S. \]
Then.
\[ d\vec{r}\mid_{\partial R}^{}\,\,=\left[ \begin{matrix} \frac{\partial x}{\partial s}& \frac{\partial x}{\partial t}\\ \frac{\partial y}{\partial s}& \frac{\partial y}{\partial t}\\ \frac{\partial z}{\partial s}& \frac{\partial z}{\partial t}\\ \end{matrix} \right] \left[ \begin{array}{c} ds\\ dt\\ \end{array} \right] \,\,=\left[ \begin{array}{c} \frac{\partial x}{\partial s}ds+\frac{\partial x}{\partial t}dt\\ \frac{\partial y}{\partial s}ds+\frac{\partial y}{\partial t}dt\\ \frac{\partial z}{\partial s}ds+\frac{\partial z}{\partial t}dt\\ \end{array} \right] \,\,=\left[ \begin{array}{c} \frac{\partial x}{\partial s}\\ \frac{\partial y}{\partial s}\\ \frac{\partial z}{\partial s}\\ \end{array} \right] ds+\left[ \begin{array}{c} \frac{\partial x}{\partial t}\\ \frac{\partial y}{\partial t}\\ \frac{\partial z}{\partial t}\\ \end{array} \right] dt\,\,=\frac{\partial \vec{r}}{\partial s}ds+\frac{\partial \vec{r}}{\partial t}dt \]
Hence.
\[ \int_{\partial S}{\vec{F}·}d\vec{r}=\int_{\partial S}{\left( \vec{F}·\frac{\partial \vec{r}}{\partial s}ds+\vec{F}·\frac{\partial \vec{r}}{\partial s} \right)} \]
We define a 2-dimensional vector field \(G=(G1,G2)\) on the s,t, plane by
\[ G_1=\vec{F}\,\,·\,\,\frac{\partial \vec{r}}{\partial s}\,\, and\,\, G_2=\vec{F}\,\,·\,\,\frac{\partial \vec{r}}{\partial t} \]
Therefore, we put G into the original line integral
\[ \int_{\partial S}{\vec{F}\,\,·\,\,d\vec{r}=}\int_{\partial R}{\left( G_1ds+G_2dt \right) =\int_R{\begin{array}{c} \left( \frac{\partial G_2}{\partial s}-\frac{\partial G_1}{\partial t} \right) dsdt\,\,,\\ \end{array}}\,\,} \]
\[ \int_{\partial S}{\vec{F}\,\,·\,\,d\vec{r}=}\int_{\partial R}{\left( G_1ds+G_2dt \right) \,\,} \]
On the other hand.
\[ \iint_S{curl\,\,\vec{F}\,\,·\,\,d\vec{S}\,\,=\,\,\iint_R{curl\,\,\vec{F}\mid_{\vec{r}}^{}·\frac{\partial \vec{r}}{\partial s}\times \frac{\partial \vec{r}}{\partial t}dsdt}} \]
We expand it, get
\[ curl\,\,\vec{F}\mid_{\vec{r}}^{}\cdot \frac{\partial \vec{r}}{\partial s}\times \frac{\partial \vec{r}}{\partial t}\,\,=\,\,\left| \begin{matrix} \frac{\partial F_3}{\partial y}-\frac{\partial F_2}{\partial z}& \frac{\partial F_1}{\partial z}-\frac{\partial F_3}{\partial x}& \frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}\\ \frac{\partial x}{\partial s}& \frac{\partial y}{\partial s}& \frac{\partial z}{\partial s}\\ \frac{\partial x}{\partial t}& \frac{\partial y}{\partial t}& \frac{\partial z}{\partial t}\\ \end{matrix} \right| \]
\[ =\frac{\partial \vec{F}}{\partial s}·\frac{\partial \vec{r}}{\partial t}-\frac{\partial \vec{F}}{\partial t}·\frac{\partial \vec{r}}{\partial s}\,\,=\frac{\partial G_2}{\partial s}-\frac{\partial G_1}{\partial t} \]
Hence.
\[ \int_R{curl\,\,F\mid_{\vec{r}}^{}\cdot \frac{\partial \vec{r}}{\partial s}}\times \frac{\partial \vec{r}}{\partial t}\,\,dsdt\,\,=\,\,\int_R{\begin{array}{c} \left( \frac{\partial G_2}{\partial s}-\frac{\partial G_1}{\partial t} \right) dsdt\,\,\\ \end{array}} \]
For the line integral part,we have
\[ \int_{\partial S}{\vec{F}\,\,·\,\,d\vec{r}=}\int_{\partial R}{\begin{array}{c} \left( G_1ds+G_2dt \right) \,\,\\ \end{array}} \]
Use Green's Theorem, we know
\[ \int_{\partial R}{\begin{array}{c} \left( G_1ds+G_2dt \right)\\ \end{array}}=\int_R{\begin{array}{c} \left( \frac{\partial G_2}{\partial s}-\frac{\partial G_1}{\partial t} \right) dsdt\,\,,\\ \end{array}} \]
So, we can conclude that
\[ \int_{\partial S}{\vec{F}·}d\vec{r}=\int_R{\begin{array}{c} \left( \frac{\partial G_2}{\partial s}-\frac{\partial G_1}{\partial t} \right) dsdt=\int_R{curl\,\,F\mid_{\vec{r}}^{}\cdot \frac{\partial \vec{r}}{\partial s}}\times \frac{\partial \vec{r}}{\partial t}\\ \end{array}}dsdt=\iint_S{curl\,\,F\,\,·\,\,d\vec{S}} \]
Thus, we finished our proof of Stokes' Theorem.
I have listened for so many times that the course: Machine Learning
by Andrew Ng is one of the best introductory course for machine
learning. Now, I have finished the first two week's classed and pass the
first programming project. I truly fathom out the deliberate design of
this course. The passion and meticulous designed project impress me as
well. It is so particular that I feel like someone is teaching me
hand-by-hand. Coursera uses a kind of judging method which is not like
the common OJ that you upload your program and they run it and test it
with their test data. Coursera uses an aggregate local submit module
that can do all the stuff. You just need to generate a token that linked
to your coursera account so that it can upload your progress. It is so
cooooool!!!!!! 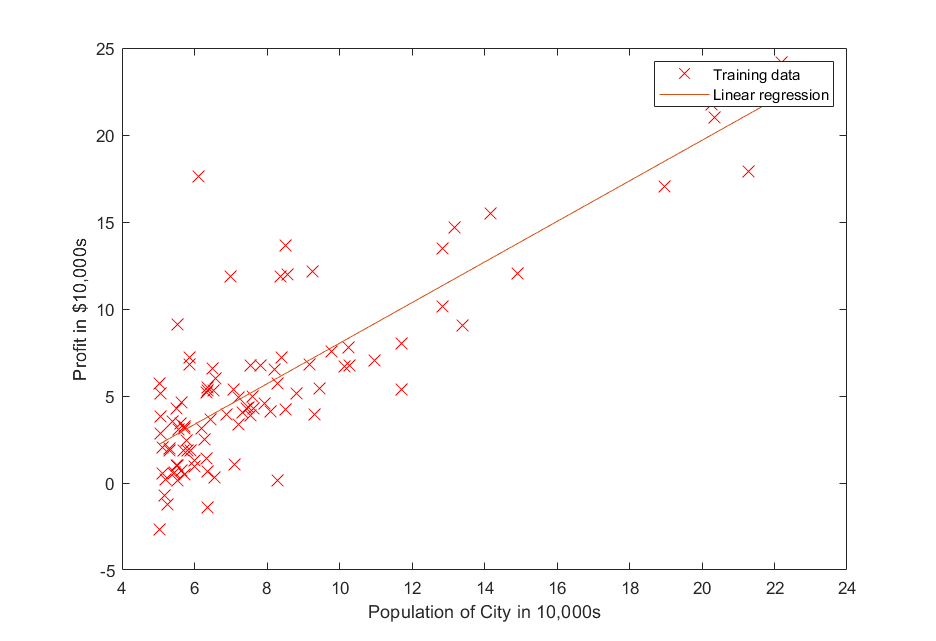
 ##### Potential Submit Problem Once
I tried to submit the program, it says
##### Potential Submit Problem Once
I tried to submit the program, it says  According to
https://blog.csdn.net/qq_44498043/article/details/105904715 and
https://blog.csdn.net/weixin_45923568/article/details/104193579 , I
found out that the error is caused by the vulnerable grammar that it
used before. And in the latest version of matlab, matlab banned those
kinds of grammar in order to increase the stability. So all we need is
to go to the coursera website and download the new version of submit
module.
According to
https://blog.csdn.net/qq_44498043/article/details/105904715 and
https://blog.csdn.net/weixin_45923568/article/details/104193579 , I
found out that the error is caused by the vulnerable grammar that it
used before. And in the latest version of matlab, matlab banned those
kinds of grammar in order to increase the stability. So all we need is
to go to the coursera website and download the new version of submit
module.
%% Initialization
clear ; close all; clc
%% ==================== Part 1: Basic Function ====================
% Complete warmUpExercise.m
fprintf('Running warmUpExercise ... \n');
fprintf('5x5 Identity Matrix: \n');
warmUpExercise()
fprintf('Program paused. Press enter to continue.\n');
pause;
%% ======================= Part 2: Plotting =======================
fprintf('Plotting Data ...\n')
data = load('ex1data1.txt');
X = data(:, 1); y = data(:, 2);
m = length(y); % number of training examples
% Plot Data
% Note: You have to complete the code in plotData.m
plotData(X, y);
fprintf('Program paused. Press enter to continue.\n');
pause;
%% =================== Part 3: Cost and Gradient descent ===================
X = [ones(m, 1), data(:,1)]; % Add a column of ones to x
theta = zeros(2, 1); % initialize fitting parameters
% Some gradient descent settings
iterations = 1500;
alpha = 0.01;
fprintf('\nTesting the cost function ...\n')
% compute and display initial cost
J = computeCost(X, y, theta);
fprintf('With theta = [0 ; 0]\nCost computed = %f\n', J);
fprintf('Expected cost value (approx) 32.07\n');
% further testing of the cost function
J = computeCost(X, y, [-1 ; 2]);
fprintf('\nWith theta = [-1 ; 2]\nCost computed = %f\n', J);
fprintf('Expected cost value (approx) 54.24\n');
fprintf('Program paused. Press enter to continue.\n');
pause;
fprintf('\nRunning Gradient Descent ...\n')
% run gradient descent
theta = gradientDescent(X, y, theta, alpha, iterations);
% print theta to screen
fprintf('Theta found by gradient descent:\n');
fprintf('%f\n', theta);
fprintf('Expected theta values (approx)\n');
fprintf(' -3.6303\n 1.1664\n\n');
% Plot the linear fit
hold on; % keep previous plot visible
plot(X(:,2), X*theta, '-')
legend('Training data', 'Linear regression')
hold off % don't overlay any more plots on this figure
% Predict values for population sizes of 35,000 and 70,000
predict1 = [1, 3.5] *theta;
fprintf('For population = 35,000, we predict a profit of %f\n',...
predict1*10000);
predict2 = [1, 7] * theta;
fprintf('For population = 70,000, we predict a profit of %f\n',...
predict2*10000);
fprintf('Program paused. Press enter to continue.\n');
pause;
%% ============= Part 4: Visualizing J(theta_0, theta_1) =============
fprintf('Visualizing J(theta_0, theta_1) ...\n')
% Grid over which we will calculate J
theta0_vals = linspace(-10, 10, 100);
theta1_vals = linspace(-1, 4, 100);
% initialize J_vals to a matrix of 0's
J_vals = zeros(length(theta0_vals), length(theta1_vals));
% Fill out J_vals
for i = 1:length(theta0_vals)
for j = 1:length(theta1_vals)
t = [theta0_vals(i); theta1_vals(j)];
J_vals(i,j) = computeCost(X, y, t);
end
end
% Because of the way meshgrids work in the surf command, we need to
% transpose J_vals before calling surf, or else the axes will be flipped
J_vals = J_vals';
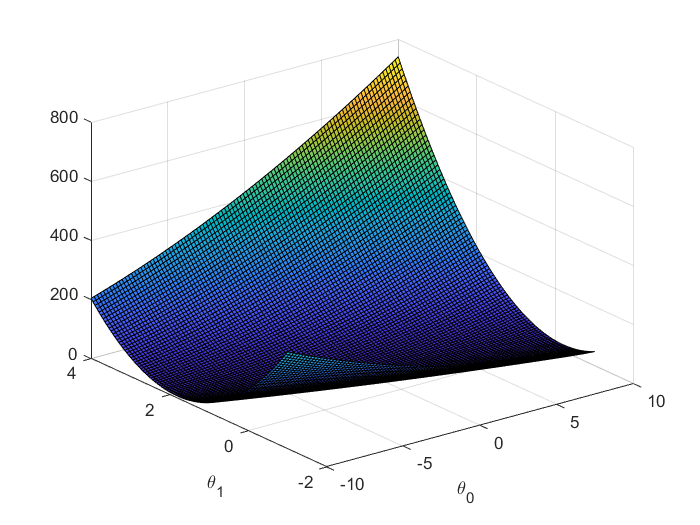
% Surface plot
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel('\theta_0'); ylabel('\theta_1');
% Contour plot
figure;
% Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20))
xlabel('\theta_0'); ylabel('\theta_1');
hold on;
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);
function J = computeCost(X, y, theta)
%COMPUTECOST Compute cost for linear regression
% J = COMPUTECOST(X, y, theta) computes the cost of using theta as the
% parameter for linear regression to fit the data points in X and y
% Initialize some useful values
m = length(y); % number of training examples
% You need to return the following variables correctly
J = 0;
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
% You should set J to the cost.
X_pd=zeros(m,1);
X_pd=X*theta;
J=sum((y-X_pd).^2);
J=J./(2.*m);
% =========================================================================
endfunction [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
% theta = GRADIENTDESCENT(X, y, theta, alpha, num_iters) updates theta by
% taking num_iters gradient steps with learning rate alpha
% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
% ====================== YOUR CODE HERE ======================
% Instructions: Perform a single gradient step on the parameter vector
% theta.
%
% Hint: While debugging, it can be useful to print out the values
% of the cost function (computeCost) and gradient here.
%
theta=theta-alpha*(1/m)*X'*(X*theta-y);
% ============================================================
% Save the cost J in every iteration
J_history(iter) = computeCost(X, y, theta);
end
end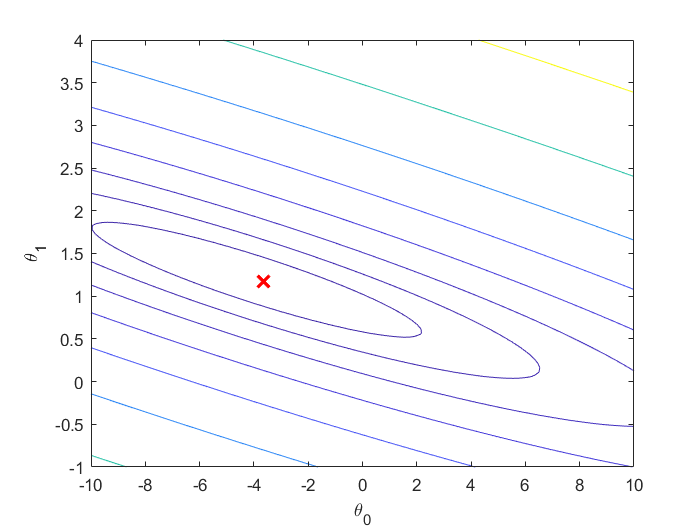

%% ================ Part 1: Feature Normalization ================
%% Clear and Close Figures
clear ; close all; clc
fprintf('Loading data ...\n');
%% Load Data
data = load('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
m = length(y);
% Print out some data points
fprintf('First 10 examples from the dataset: \n');
fprintf(' x = [%.0f %.0f], y = %.0f \n', [X(1:10,:) y(1:10,:)]');
fprintf('Program paused. Press enter to continue.\n');
pause;
% Scale features and set them to zero mean
fprintf('Normalizing Features ...\n');
[X mu sigma] = featureNormalize(X);
% Add intercept term to X
X = [ones(m, 1) X];
%% ================ Part 2: Gradient Descent ================
% ====================== YOUR CODE HERE ======================
% Instructions: We have provided you with the following starter
% code that runs gradient descent with a particular
% learning rate (alpha).
%
% Your task is to first make sure that your functions -
% computeCost and gradientDescent already work with
% this starter code and support multiple variables.
%
% After that, try running gradient descent with
% different values of alpha and see which one gives
% you the best result.
%
% Finally, you should complete the code at the end
% to predict the price of a 1650 sq-ft, 3 br house.
%
% Hint: By using the 'hold on' command, you can plot multiple
% graphs on the same figure.
%
% Hint: At prediction, make sure you do the same feature normalization.
%
fprintf('Running gradient descent ...\n');
% Choose some alpha value
alpha = 0.01;
num_iters = 400;
% Init Theta and Run Gradient Descent
theta = zeros(3, 1);
[theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters);
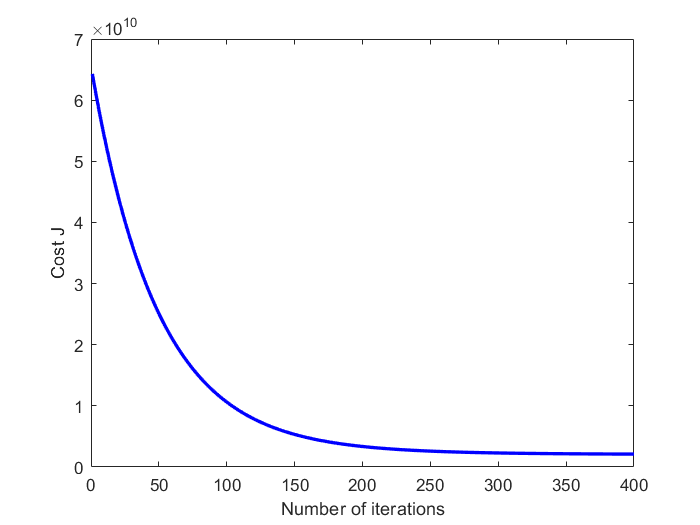
% Plot the convergence graph
figure;
plot(1:numel(J_history), J_history, '-b', 'LineWidth', 2);
xlabel('Number of iterations');
ylabel('Cost J');
% Display gradient descent's result
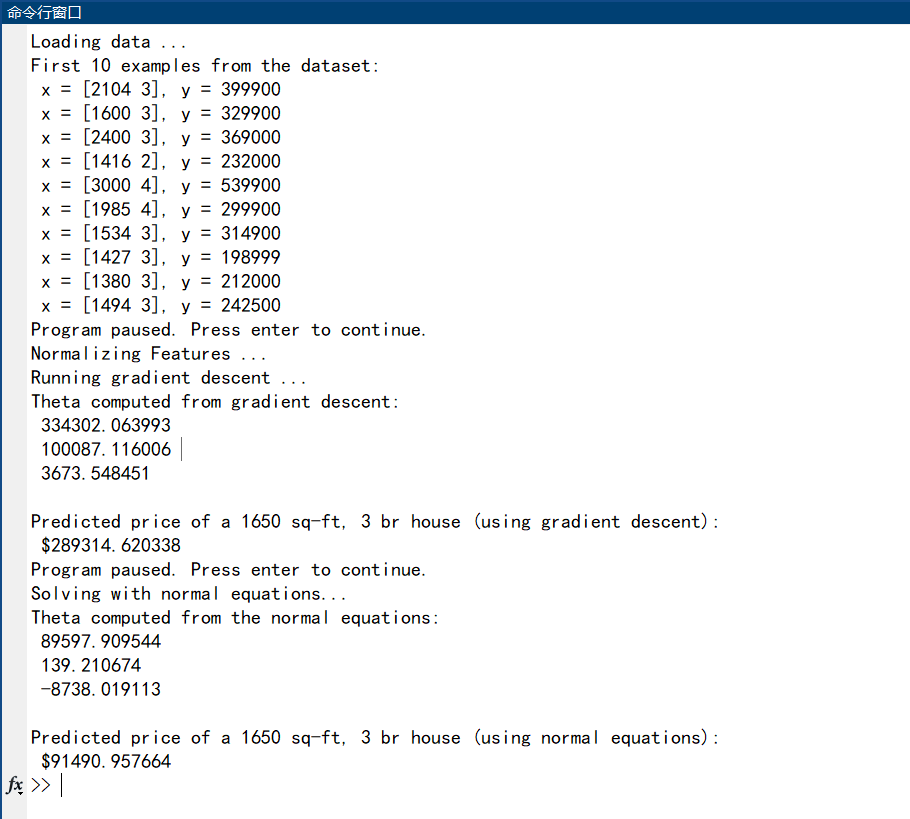
fprintf('Theta computed from gradient descent: \n');
fprintf(' %f \n', theta);
fprintf('\n');
% Estimate the price of a 1650 sq-ft, 3 br house
% ====================== YOUR CODE HERE ======================
% Recall that the first column of X is all-ones. Thus, it does
% not need to be normalized.
price = 0; % You should change this
X_test1=[1,(1650-mu(1,1))./sigma(1,1),(3-mu(1,2))./sigma(1,2)];
price=X_test1*theta;
% ============================================================
fprintf(['Predicted price of a 1650 sq-ft, 3 br house ' ...
'(using gradient descent):\n $%f\n'], price);
fprintf('Program paused. Press enter to continue.\n');
pause;
%% ================ Part 3: Normal Equations ================
fprintf('Solving with normal equations...\n');
% ====================== YOUR CODE HERE ======================
% Instructions: The following code computes the closed form
% solution for linear regression using the normal
% equations. You should complete the code in
% normalEqn.m
%
% After doing so, you should complete this code
% to predict the price of a 1650 sq-ft, 3 br house.
%
%% Load Data
data = csvread('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
m = length(y);
% Add intercept term to X
X = [ones(m, 1) X];
% Calculate the parameters from the normal equation
theta = normalEqn(X, y);
% Display normal equation's result
fprintf('Theta computed from the normal equations: \n');
fprintf(' %f \n', theta);
fprintf('\n');
% Estimate the price of a 1650 sq-ft, 3 br house
% ====================== YOUR CODE HERE ======================
price = 0; % You should change this
X_test2=[1,(1650-mu(1,1))./sigma(1,1),(3-mu(1,2))./sigma(1,2)];
price=X_test2*theta;
% ============================================================
fprintf(['Predicted price of a 1650 sq-ft, 3 br house ' ...
'(using normal equations):\n $%f\n'], price);
%% ================ Part 1: Feature Normalization ================
%% Clear and Close Figures
clear ; close all; clc
fprintf('Loading data ...\n');
%% Load Data
data = load('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
m = length(y);
% Print out some data points
fprintf('First 10 examples from the dataset: \n');
fprintf(' x = [%.0f %.0f], y = %.0f \n', [X(1:10,:) y(1:10,:)]');
fprintf('Program paused. Press enter to continue.\n');
pause;
% Scale features and set them to zero mean
fprintf('Normalizing Features ...\n');
[X mu sigma] = featureNormalize(X);
% Add intercept term to X
X = [ones(m, 1) X];
%% ================ Part 2: Gradient Descent ================
% ====================== YOUR CODE HERE ======================
% Instructions: We have provided you with the following starter
% code that runs gradient descent with a particular
% learning rate (alpha).
%
% Your task is to first make sure that your functions -
% computeCost and gradientDescent already work with
% this starter code and support multiple variables.
%
% After that, try running gradient descent with
% different values of alpha and see which one gives
% you the best result.
%
% Finally, you should complete the code at the end
% to predict the price of a 1650 sq-ft, 3 br house.
%
% Hint: By using the 'hold on' command, you can plot multiple
% graphs on the same figure.
%
% Hint: At prediction, make sure you do the same feature normalization.
%
fprintf('Running gradient descent ...\n');
% Choose some alpha value
alpha = 0.01;
num_iters = 400;
% Init Theta and Run Gradient Descent
theta = zeros(3, 1);
[theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters);
% Plot the convergence graph
figure;
plot(1:numel(J_history), J_history, '-b', 'LineWidth', 2);
xlabel('Number of iterations');
ylabel('Cost J');
% Display gradient descent's result
fprintf('Theta computed from gradient descent: \n');
fprintf(' %f \n', theta);
fprintf('\n');
% Estimate the price of a 1650 sq-ft, 3 br house
% ====================== YOUR CODE HERE ======================
% Recall that the first column of X is all-ones. Thus, it does
% not need to be normalized.
price = 0; % You should change this
X_test1=[1,(1650-mu(1,1))./sigma(1,1),(3-mu(1,2))./sigma(1,2)];
price=X_test1*theta;
% ============================================================
fprintf(['Predicted price of a 1650 sq-ft, 3 br house ' ...
'(using gradient descent):\n $%f\n'], price);
fprintf('Program paused. Press enter to continue.\n');
pause;
%% ================ Part 3: Normal Equations ================
fprintf('Solving with normal equations...\n');
% ====================== YOUR CODE HERE ======================
% Instructions: The following code computes the closed form
% solution for linear regression using the normal
% equations. You should complete the code in
% normalEqn.m
%
% After doing so, you should complete this code
% to predict the price of a 1650 sq-ft, 3 br house.
%
%% Load Data
data = csvread('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
m = length(y);
% Add intercept term to X
X = [ones(m, 1) X];
% Calculate the parameters from the normal equation
theta = normalEqn(X, y);
% Display normal equation's result
fprintf('Theta computed from the normal equations: \n');
fprintf(' %f \n', theta);
fprintf('\n');
% Estimate the price of a 1650 sq-ft, 3 br house
% ====================== YOUR CODE HERE ======================
price = 0; % You should change this
X_test2=[1,(1650-mu(1,1))./sigma(1,1),(3-mu(1,2))./sigma(1,2)];
price=X_test2*theta;
% ============================================================
fprintf(['Predicted price of a 1650 sq-ft, 3 br house ' ...
'(using normal equations):\n $%f\n'], price);
%% ================ Part 1: Feature Normalization ================
%% Clear and Close Figures
clear ; close all; clc
fprintf('Loading data ...\n');
%% Load Data
data = load('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
m = length(y);
% Print out some data points
fprintf('First 10 examples from the dataset: \n');
fprintf(' x = [%.0f %.0f], y = %.0f \n', [X(1:10,:) y(1:10,:)]');
fprintf('Program paused. Press enter to continue.\n');
pause;
% Scale features and set them to zero mean
fprintf('Normalizing Features ...\n');
[X mu sigma] = featureNormalize(X);
% Add intercept term to X
X = [ones(m, 1) X];
%% ================ Part 2: Gradient Descent ================
% ====================== YOUR CODE HERE ======================
% Instructions: We have provided you with the following starter
% code that runs gradient descent with a particular
% learning rate (alpha).
%
% Your task is to first make sure that your functions -
% computeCost and gradientDescent already work with
% this starter code and support multiple variables.
%
% After that, try running gradient descent with
% different values of alpha and see which one gives
% you the best result.
%
% Finally, you should complete the code at the end
% to predict the price of a 1650 sq-ft, 3 br house.
%
% Hint: By using the 'hold on' command, you can plot multiple
% graphs on the same figure.
%
% Hint: At prediction, make sure you do the same feature normalization.
%
fprintf('Running gradient descent ...\n');
% Choose some alpha value
alpha = 0.01;
num_iters = 400;
% Init Theta and Run Gradient Descent
theta = zeros(3, 1);
[theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters);
% Plot the convergence graph
figure;
plot(1:numel(J_history), J_history, '-b', 'LineWidth', 2);
xlabel('Number of iterations');
ylabel('Cost J');
% Display gradient descent's result
fprintf('Theta computed from gradient descent: \n');
fprintf(' %f \n', theta);
fprintf('\n');
% Estimate the price of a 1650 sq-ft, 3 br house
% ====================== YOUR CODE HERE ======================
% Recall that the first column of X is all-ones. Thus, it does
% not need to be normalized.
price = 0; % You should change this
X_test1=[1,(1650-mu(1,1))./sigma(1,1),(3-mu(1,2))./sigma(1,2)];
price=X_test1*theta;
% ============================================================
fprintf(['Predicted price of a 1650 sq-ft, 3 br house ' ...
'(using gradient descent):\n $%f\n'], price);
fprintf('Program paused. Press enter to continue.\n');
pause;
%% ================ Part 3: Normal Equations ================
fprintf('Solving with normal equations...\n');
% ====================== YOUR CODE HERE ======================
% Instructions: The following code computes the closed form
% solution for linear regression using the normal
% equations. You should complete the code in
% normalEqn.m
%
% After doing so, you should complete this code
% to predict the price of a 1650 sq-ft, 3 br house.
%
%% Load Data
data = csvread('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
m = length(y);
% Add intercept term to X
X = [ones(m, 1) X];
% Calculate the parameters from the normal equation
theta = normalEqn(X, y);
% Display normal equation's result
fprintf('Theta computed from the normal equations: \n');
fprintf(' %f \n', theta);
fprintf('\n');
% Estimate the price of a 1650 sq-ft, 3 br house
% ====================== YOUR CODE HERE ======================
price = 0; % You should change this
X_test2=[1,(1650-mu(1,1))./sigma(1,1),(3-mu(1,2))./sigma(1,2)];
price=X_test2*theta;
% ============================================================
fprintf(['Predicted price of a 1650 sq-ft, 3 br house ' ...
'(using normal equations):\n $%f\n'], price);
%% ================ Part 1: Feature Normalization ================
%% Clear and Close Figures
clear ; close all; clc
fprintf('Loading data ...\n');
%% Load Data
data = load('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
m = length(y);
% Print out some data points
fprintf('First 10 examples from the dataset: \n');
fprintf(' x = [%.0f %.0f], y = %.0f \n', [X(1:10,:) y(1:10,:)]');
fprintf('Program paused. Press enter to continue.\n');
pause;
% Scale features and set them to zero mean
fprintf('Normalizing Features ...\n');
[X mu sigma] = featureNormalize(X);
% Add intercept term to X
X = [ones(m, 1) X];
%% ================ Part 2: Gradient Descent ================
% ====================== YOUR CODE HERE ======================
% Instructions: We have provided you with the following starter
% code that runs gradient descent with a particular
% learning rate (alpha).
%
% Your task is to first make sure that your functions -
% computeCost and gradientDescent already work with
% this starter code and support multiple variables.
%
% After that, try running gradient descent with
% different values of alpha and see which one gives
% you the best result.
%
% Finally, you should complete the code at the end
% to predict the price of a 1650 sq-ft, 3 br house.
%
% Hint: By using the 'hold on' command, you can plot multiple
% graphs on the same figure.
%
% Hint: At prediction, make sure you do the same feature normalization.
%
fprintf('Running gradient descent ...\n');
% Choose some alpha value
alpha = 0.01;
num_iters = 400;
% Init Theta and Run Gradient Descent
theta = zeros(3, 1);
[theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters);
% Plot the convergence graph
figure;
plot(1:numel(J_history), J_history, '-b', 'LineWidth', 2);
xlabel('Number of iterations');
ylabel('Cost J');
% Display gradient descent's result
fprintf('Theta computed from gradient descent: \n');
fprintf(' %f \n', theta);
fprintf('\n');
% Estimate the price of a 1650 sq-ft, 3 br house
% ====================== YOUR CODE HERE ======================
% Recall that the first column of X is all-ones. Thus, it does
% not need to be normalized.
price = 0; % You should change this
X_test1=[1,(1650-mu(1,1))./sigma(1,1),(3-mu(1,2))./sigma(1,2)];
price=X_test1*theta;
% ============================================================
fprintf(['Predicted price of a 1650 sq-ft, 3 br house ' ...
'(using gradient descent):\n $%f\n'], price);
fprintf('Program paused. Press enter to continue.\n');
pause;
%% ================ Part 3: Normal Equations ================
fprintf('Solving with normal equations...\n');
% ====================== YOUR CODE HERE ======================
% Instructions: The following code computes the closed form
% solution for linear regression using the normal
% equations. You should complete the code in
% normalEqn.m
%
% After doing so, you should complete this code
% to predict the price of a 1650 sq-ft, 3 br house.
%
%% Load Data
data = csvread('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
m = length(y);
% Add intercept term to X
X = [ones(m, 1) X];
% Calculate the parameters from the normal equation
theta = normalEqn(X, y);
% Display normal equation's result
fprintf('Theta computed from the normal equations: \n');
fprintf(' %f \n', theta);
fprintf('\n');
% Estimate the price of a 1650 sq-ft, 3 br house
% ====================== YOUR CODE HERE ======================
price = 0; % You should change this
X_test2=[1,(1650-mu(1,1))./sigma(1,1),(3-mu(1,2))./sigma(1,2)];
price=X_test2*theta;
% ============================================================
fprintf(['Predicted price of a 1650 sq-ft, 3 br house ' ...
'(using normal equations):\n $%f\n'], price);
function [theta] = normalEqn(X, y)
%NORMALEQN Computes the closed-form solution to linear regression
% NORMALEQN(X,y) computes the closed-form solution to linear
% regression using the normal equations.
theta = zeros(size(X, 2), 1);
% ====================== YOUR CODE HERE ======================
% Instructions: Complete the code to compute the closed form solution
% to linear regression and put the result in theta.
%
% ---------------------- Sample Solution ----------------------
theta = pinv(transpose(X)*X)*transpose(X)*y;
% -------------------------------------------------------------
% ============================================================
end
I am afraid of being a simp of her, not because I don't love her but because I love her so deeply that I can't afford the cost of losing the unparalleledly and weakly existing relationship with her.
忽然发现在学校这种全天学习,学和放松娱乐整合成一个整体的状态非常高效且舒适。总而言之就是一直在学并且放松,从早上一直到睡觉,并不像有些人想的那样,什么时候到什么时候全学,然后开始玩知道睡觉,我觉得这种学习时间的分隔感会降低学习效率。 此外,在看了那么多北师大实验国际部的申请成功案例之后,我终于意识到了一个事情,就是实验人均一个各种各样的科研,这才是他们成功的关键。 爱一个人却不敢接近,并不是因为爱得不够深;而是因为爱的足够深从而害怕失去这易碎且美好的挂念。
An interesting "Hello World" in OpenCV. It invokes the camera and recognizes hands. Then, it uses the coordinates of these nodes in hands to draw the real time hands frameworks.
Here comes the code:
import cv2
import mediapipe as mp
cap=cv2.VideoCapture(0)
mpHands= mp.solutions.hands
hands = mpHands.Hands()
mpDraw= mp.solutions.drawing_utils
while True:
ret, img =cap.read()
if ret:
imgRGB=cv2.cvtColor(img,cv2.COLOR_BGR2RGB)
result=hands.process(imgRGB)
#print(result.multi_hand_landmarks)
if result.multi_hand_landmarks:
for handLms in result.multi_hand_landmarks:
mpDraw.draw_landmarks(img,handLms,mpHands.HAND_CONNECTIONS)
cv2.imshow('img',img)
if cv2.waitKey(1) == ord('q'):
break
https://www.bilibili.com/video/BV1w44y1j7y3
观Pioneer年度最佳论文们有感。 在美本申请领域,人们看起来的强度(指除了GPA以外的,例如标化,水竞赛,活动等等),其实并不像高考一样,纯和你的智力与努力程度成正比。美本申请的这些东西,其实更取决于起步时间。就比如说高一开学的时候,有的人托福115,有的人还没开始学,像托福,ACT,SAT,高中生的那些所谓的”竞赛“,其实并不需要智力和方法,就是看学习时间的长短和积累。而当起步晚的学生们在奋力学标化的时候,那些起步早的人,就可以拿出时间去搞活动,搞竞赛,搞”科研“去了。至于美高学生,那就是起步更早的,所以就,从美本申请的角度来看更成功。 所以我想对现在迷茫和焦虑的人说,你虽然感觉自己没有有一些人强,并不是因为你的能力不行,而是你的起步时间太晚了,所以不要担心,美本其实都差不多,本科大家都是一样的,好好学习,最后体现的才是大家真实的实力。
啊 后天就考托福了 不过想想也没必要紧张,反正我要求不高,又不申夏校,只要比之前的拼分高一点就行。
假期还感兴趣了一些别的,比如星际争霸的re-take;日本那个全能房屋改造,看那些现代和风的建筑和装修真的很喜欢,以后一定要想办法多参观这种和风一户建。此外还有戏腔,非传统京剧,虽然是那些流行的比如探窗啊赤玲啥的,但是我觉得挺好听的。
开学了之后就可以开始稍微正常一点,闲适一点了,可惜要一遍刷AP,准备开学考。之后还得一边背ACT单词,一边读要读的Lolita 高堡奇人和历史书了,,。还要想办法抽出时间继续学习ML。。。。啊 还有物理C。。淦了